FDFD mode solver#
We also have a FDFD mode solver.
Waveguides#
Guided Electromagnetic modes are the ones that have an effective index larger than the cladding of the waveguide
Here is a waveguide of Silicon (n=3.4) surrounded by SiO2 (n=1.44) cladding
For a 220 nm height x 450 nm width the effective index is 2.466
import gdsfactory as gf
import gplugins.tidy3d as gt
import matplotlib.pyplot as plt
import numpy as np
from gdsfactory.generic_tech import get_generic_pdk
gf.config.rich_output()
PDK = get_generic_pdk()
PDK.activate()
nm = 1e-3
wg_width = 0.5
wavelength = 1.55
core_thickness = 0.22
slab_thickness = 0.0
core_material = "si" # can be a string or a number with the refractive index
clad_material = "sio2"
slab_thickness_rib = 0.15
nitride_thickness = 0.4
strip = gt.modes.Waveguide(
wavelength=wavelength,
core_width=wg_width,
core_thickness=core_thickness,
slab_thickness=slab_thickness,
core_material=core_material,
clad_material=clad_material,
num_modes=2,
sidewall_angle=np.deg2rad(10),
)
strip.plot_index()
<matplotlib.collections.QuadMesh object at 0x7f10cf50e690>
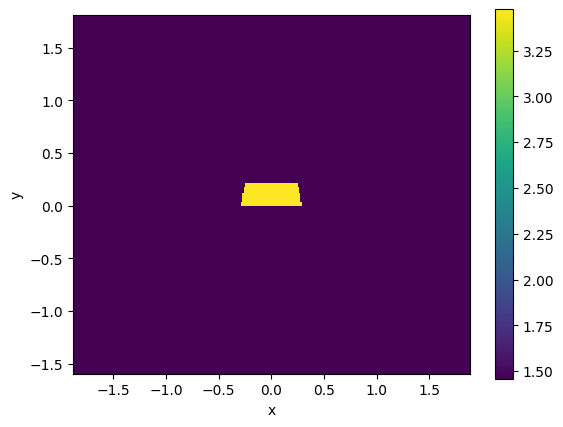
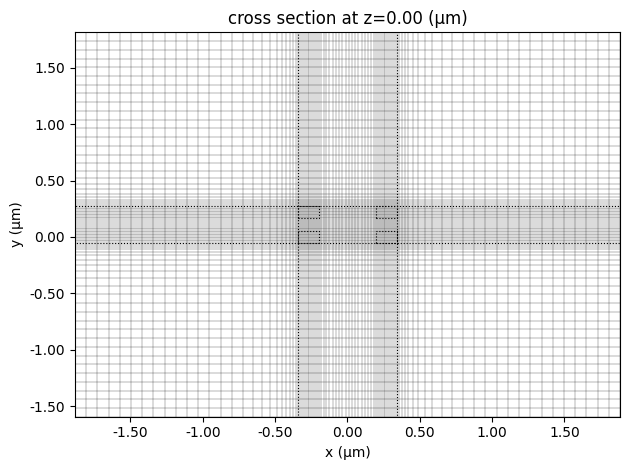
strip.plot_grid()
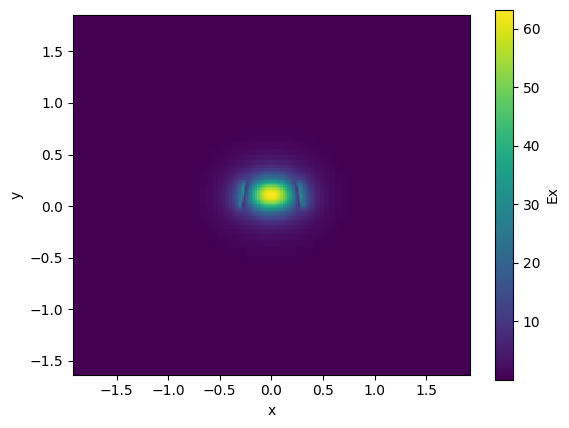
strip.plot_field(field_name="Ex", mode_index=0) # TE
06:20:38 UTC WARNING: The group index was not computed. To calculate group index, pass 'group_index_step = True' in the 'ModeSpec'.
<matplotlib.collections.QuadMesh object at 0x7f10cd022a90>
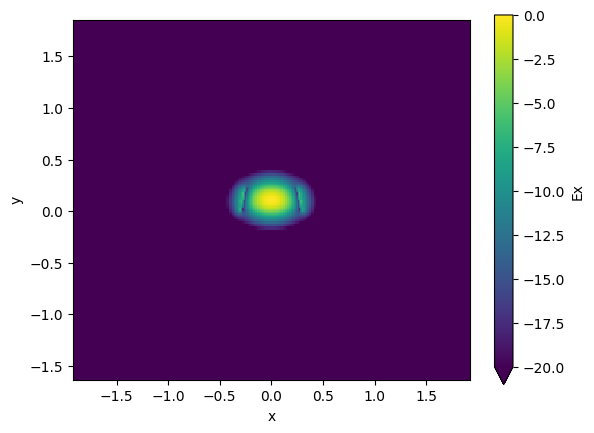
strip.plot_field(field_name="Ex", mode_index=0, value="dB") # TE
<matplotlib.collections.QuadMesh object at 0x7f10ccd5b250>
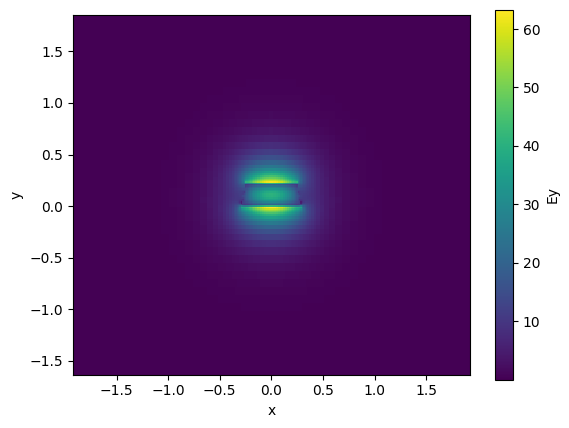
strip.plot_field(field_name="Ey", mode_index=1) # TM
<matplotlib.collections.QuadMesh object at 0x7f10ccdc8f90>
strip.n_eff
array([2.54959783+4.11062054e-05j, 1.88581037+2.04207812e-04j])
slab_thickness = 0.15
rib = gt.modes.Waveguide(
wavelength=wavelength,
core_width=wg_width,
core_thickness=core_thickness,
slab_thickness=slab_thickness,
core_material=core_material,
clad_material=clad_material,
num_modes=2,
sidewall_angle=np.deg2rad(10),
)
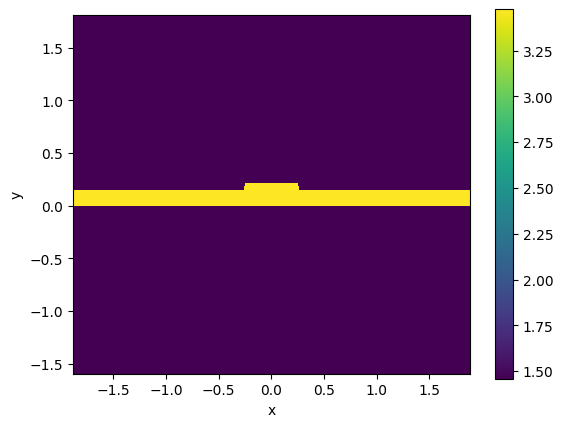
rib.plot_index()
rib.n_eff
06:20:40 UTC WARNING: Mode field at frequency index 0, mode index 1 does not decay at the plane boundaries.
array([2.67680485+3.13289436e-05j, 2.50895287+4.47976905e-05j])
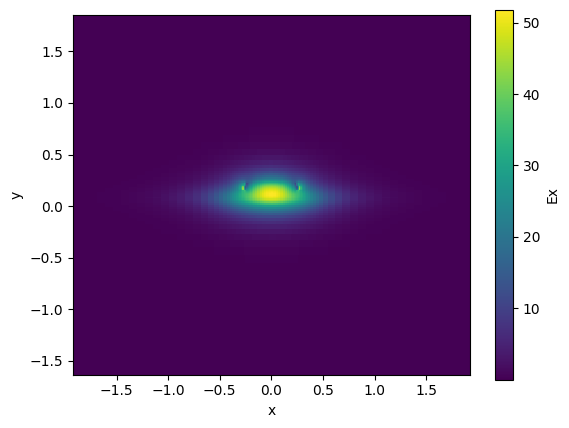
rib.plot_field(field_name="Ex", mode_index=0) # TE
<matplotlib.collections.QuadMesh object at 0x7f10cca20190>
nitride = gt.modes.Waveguide(
wavelength=wavelength,
core_width=1.0,
core_thickness=nitride_thickness,
slab_thickness=0.0,
core_material="sin", # can be a string or a number with the refractive index
clad_material="sio2",
sidewall_angle=np.deg2rad(10)
)
nitride.plot_index()
nitride.n_eff
array([1.65390492+7.63134331e-05j, 1.58330988+1.40964564e-04j])
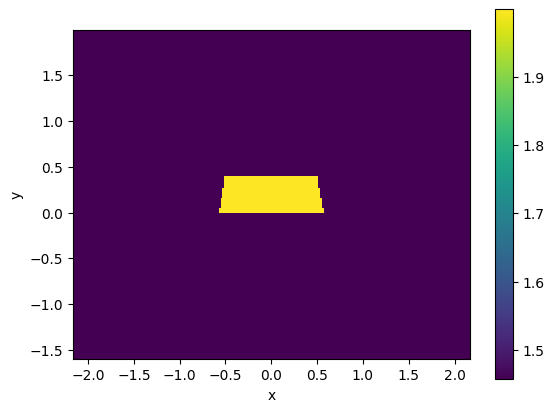
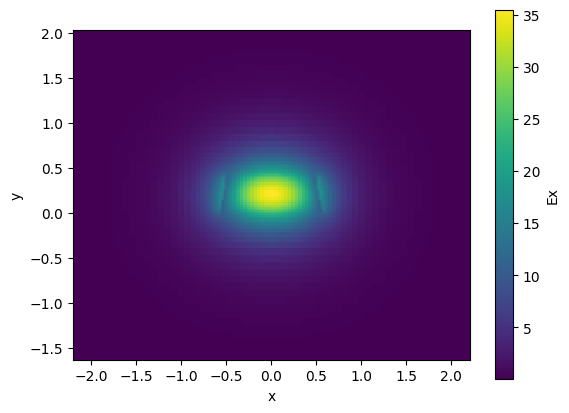
nitride.plot_field(field_name="Ex", mode_index=0) # TE
<matplotlib.collections.QuadMesh object at 0x7f10cc821010>
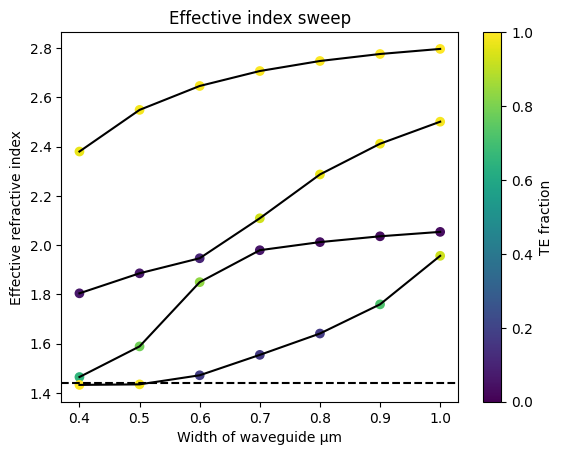
Sweep width#
You can sweep the waveguide width and compute the modes.
By increasing the waveguide width, the waveguide supports many more TE and TM modes. Where TE modes have a dominant Ex field and TM modes have larger Ey fields.
Notice that waveguides wider than 0.450 um support more than one TE mode. Therefore the maximum width for single mode operation is 0.450 um.
wg_width = 0.5
wavelength = 1.55
core_thickness = 0.22
slab_thickness = 0.0
core_material = "si" # can be a string or a number with the refractive index
clad_material = "sio2"
strip = gt.modes.Waveguide(
wavelength=wavelength,
core_width=wg_width,
core_thickness=core_thickness,
slab_thickness=slab_thickness,
core_material=core_material,
clad_material=clad_material,
num_modes=4,
sidewall_angle=np.deg2rad(10),
)
w = np.linspace(400 * nm, 1000 * nm, 7)
n_eff = gt.modes.sweep_n_eff(strip, core_width=w)
fraction_te = gt.modes.sweep_fraction_te(strip, core_width=w)
for i in range(4):
plt.plot(w, n_eff.sel(mode_index=i).real, c="k")
plt.scatter(
w, n_eff.sel(mode_index=i).real, c=fraction_te.sel(mode_index=i), vmin=0, vmax=1
)
plt.axhline(y=1.44, color="k", ls="--")
plt.colorbar().set_label("TE fraction")
plt.xlabel("Width of waveguide µm")
plt.ylabel("Effective refractive index")
plt.title("Effective index sweep")
06:20:42 UTC WARNING: Mode field at frequency index 0, mode index 3 does not decay at the plane boundaries.
06:20:44 UTC WARNING: Mode field at frequency index 0, mode index 3 does not decay at the plane boundaries.
Text(0.5, 1.0, 'Effective index sweep')
Exercises
What is the maximum width to support a single TE mode at 1310 nm?
For a Silicon Nitride (n=2) 400nm thick waveguide surrounded by SiO2 (n=1.44), what is the maximum width to support a single TE mode at 1550 nm?
For two 500x220nm Silicon waveguides surrounded by SiO2, what is the coupling length (100% coupling) for 200 nm gap?
Group index#
You can also compute the group index for a waveguide.
nm = 1e-3
wavelength = 1.55
wg_width = 0.5
core_thickness = 0.22
strip = gt.modes.Waveguide(
wavelength=wavelength,
core_width=wg_width,
slab_thickness=0.0,
core_material="si",
clad_material="sio2",
core_thickness=core_thickness,
num_modes=4,
group_index_step=10 * nm,
)
print(strip.n_group)
06:20:53 UTC WARNING: Mode field at frequency index 0, mode index 3 does not decay at the plane boundaries.
WARNING: Mode field at frequency index 1, mode index 3 does not decay at the plane boundaries.
WARNING: Mode field at frequency index 2, mode index 3 does not decay at the plane boundaries.
[4.17803969 4.08299706 2.71577378 1.50333028]
Bend modes#
You can compute bend modes specifying the bend radius.
strip_bend = gt.modes.Waveguide(
wavelength=wavelength,
core_width=wg_width,
core_thickness=core_thickness,
slab_thickness=0.0,
bend_radius=4,
core_material="si",
clad_material="sio2",
)
strip_bend.plot_field(field_name="Ex", mode_index=0) # TE
06:20:54 UTC WARNING: Mode field at frequency index 0, mode index 1 does not decay at the plane boundaries.
<matplotlib.collections.QuadMesh object at 0x7f10cf318810>
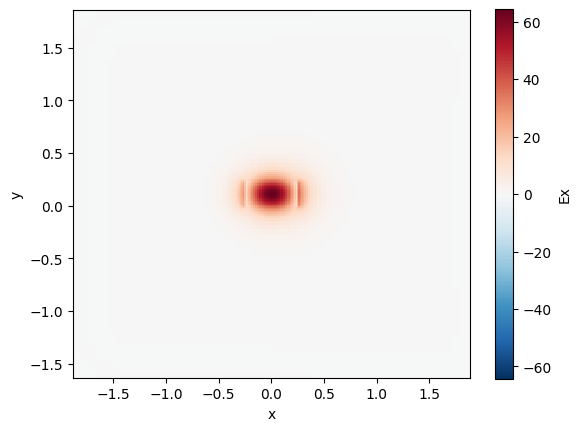
Bend loss#
You can also compute the losses coming from the mode mismatch from the bend into a straight waveguide. To compute the bend loss due to mode mismatch you can calculate the mode overlap of the straight mode and the bent mode. Because there are two mode mismatch interfaces the total loss due to mode mismatch will be squared (from bend to straight and from straight to bend).

radii = np.arange(4, 7)
bend = gt.modes.Waveguide(
wavelength=wavelength,
core_width=wg_width,
core_thickness=core_thickness,
core_material="si",
clad_material="sio2",
num_modes=1,
bend_radius=radii.min(),
)
mismatch = gt.modes.sweep_bend_mismatch(bend, radii)
plt.plot(radii, 10 * np.log10(mismatch))
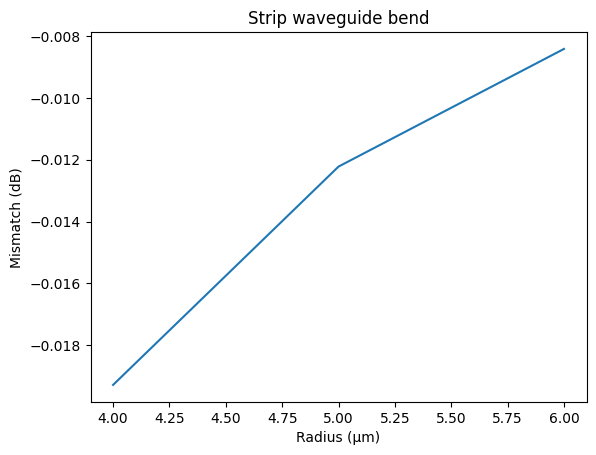
plt.title("Strip waveguide bend")
plt.xlabel("Radius (μm)")
plt.ylabel("Mismatch (dB)")
Text(0, 0.5, 'Mismatch (dB)')
dB_cm = 2 # dB/cm
length = 2 * np.pi * radii * 1e-6
propagation_loss = dB_cm * length * 1e2
print(f"Propagation loss for 2πR bend: {propagation_loss} dB")
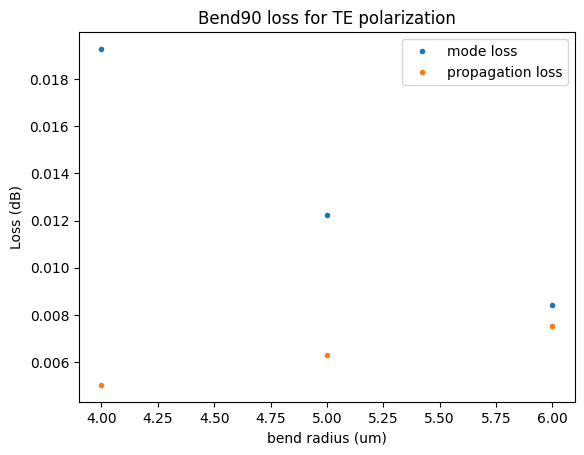
plt.title("Bend90 loss for TE polarization")
plt.plot(radii, -10 * np.log10(mismatch), ".", label="mode loss")
plt.plot(radii, propagation_loss, ".", label="propagation loss")
plt.xlabel("bend radius (um)")
plt.ylabel("Loss (dB)")
plt.legend()
Propagation loss for 2πR bend: [0.00502655 0.00628319 0.00753982] dB
<matplotlib.legend.Legend object at 0x7f10cf432bd0>
rib = gt.modes.Waveguide(
wavelength=wavelength,
core_width=wg_width,
core_thickness=core_thickness,
slab_thickness=slab_thickness_rib,
bend_radius=15,
core_material="si",
clad_material="sio2",
)
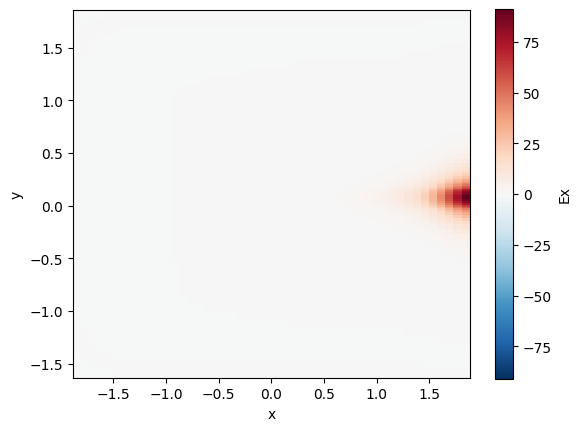
rib.plot_field(field_name="Ex", mode_index=0) # TE
06:20:57 UTC WARNING: Mode field at frequency index 0, mode index 0 does not decay at the plane boundaries.
WARNING: Mode field at frequency index 0, mode index 1 does not decay at the plane boundaries.
<matplotlib.collections.QuadMesh object at 0x7f10cf311e90>
nitride_bend = gt.modes.Waveguide(
wavelength=1.55,
core_width=1000 * nm,
core_thickness=nitride_thickness,
slab_thickness=0.0,
bend_radius=30,
core_material="sin",
clad_material="sio2",
)
nitride_bend.plot_field(field_name="Ex", mode_index=0, value="abs") # TE
<matplotlib.collections.QuadMesh object at 0x7f10cb58b7d0>

radii = np.array([30, 35, 40])
bend = gt.modes.Waveguide(
wavelength=wavelength,
core_width=1000 * nm,
core_thickness=nitride_thickness,
core_material="sin",
clad_material="sio2",
num_modes=1,
bend_radius=radii.min(),
)
mismatch = gt.modes.sweep_bend_mismatch(bend, radii)
dB_cm = 2 # dB/cm
length = 2 * np.pi * radii * 1e-6
propagation_loss = dB_cm * length * 1e2
print(f"propagation_loss for 2PI degree bend = {propagation_loss} dB")
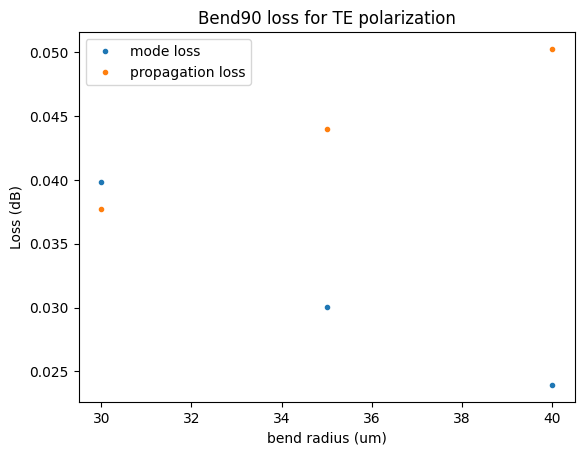
plt.title("Bend90 loss for TE polarization")
plt.plot(radii, -10 * np.log10(mismatch), ".", label="mode loss")
plt.plot(radii, propagation_loss, ".", label="propagation loss")
plt.xlabel("bend radius (um)")
plt.ylabel("Loss (dB)")
plt.legend()
propagation_loss for 2PI degree bend = [0.03769911 0.0439823 0.05026548] dB
<matplotlib.legend.Legend object at 0x7f10cb599110>
Exercises
For a 500nm wide 220nm thick Silicon waveguide surrounded by SiO2, what is the minimum bend radius to have less than 0.04dB loss for TE polarization at 1550nm?
For a 500nm wide 220nm thick Silicon waveguide surrounded by SiO2, what is the minimum bend radius to have 99% power transmission for TM polarization at 1550nm?
Waveguide coupler#
You can also compute the modes of a waveguide coupler.
ore_width[0] core_width[1]
<-------> <------->
_______ _______ _
| | | | |
| | | |
| |_____| | | core_thickness
|slab_thickness |
|_____________________| |_
<----->
gap
gap = 200 * nm
c = gt.modes.WaveguideCoupler(
wavelength=wavelength,
core_width=(wg_width, wg_width),
gap=gap,
core_thickness=core_thickness,
slab_thickness=slab_thickness,
core_material="si",
clad_material="sio2",
)
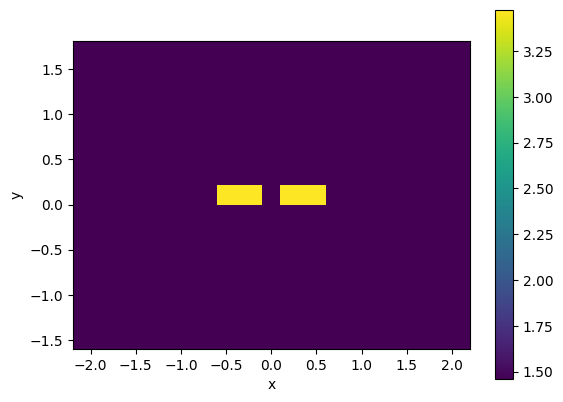
c.plot_index()
<matplotlib.collections.QuadMesh object at 0x7f10cb1c8990>
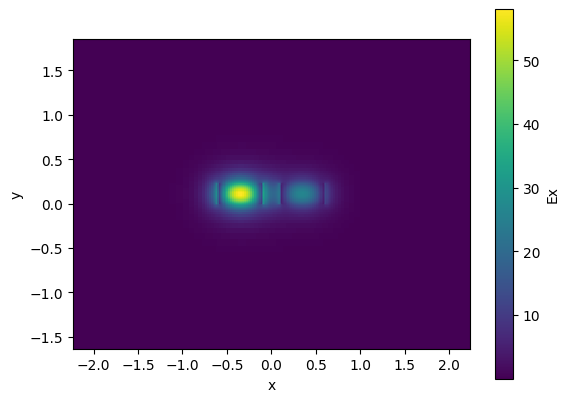
c.plot_field(field_name="Ex", mode_index=0) # TE
<matplotlib.collections.QuadMesh object at 0x7f10cb2201d0>
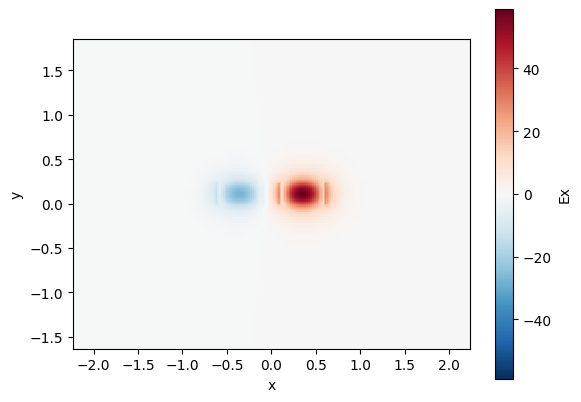
c.plot_field(field_name="Ex", mode_index=1) # TE
<matplotlib.collections.QuadMesh object at 0x7f10cb2d0f90>
coupler = gt.modes.WaveguideCoupler(
wavelength=wavelength,
core_width=(wg_width, wg_width),
gap=gap,
core_thickness=core_thickness,
slab_thickness=slab_thickness,
core_material="si",
clad_material="sio2",
num_modes=4,
)
print("\nCoupler:", coupler)
print("Effective indices:", coupler.n_eff)
print("Mode areas:", coupler.mode_area)
print("Coupling length:", coupler.coupling_length())
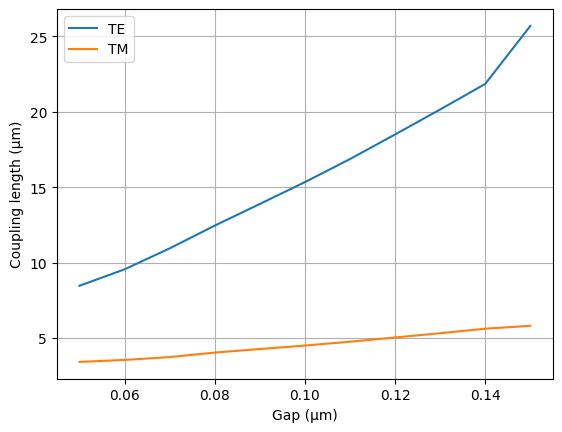
gaps = np.linspace(0.05, 0.15, 11)
lengths = gt.modes.sweep_coupling_length(coupler, gaps)
_, ax = plt.subplots(1, 1)
ax.plot(gaps, lengths)
ax.set(xlabel="Gap (μm)", ylabel="Coupling length (μm)")
ax.legend(["TE", "TM"])
ax.grid()
Coupler: WaveguideCoupler(wavelength=array(1.55), core_width=['0.5', '0.5'], core_thickness='0.22', core_material='si', clad_material='sio2', box_material=None, slab_thickness='0.0', clad_thickness=None, box_thickness=None, side_margin=None, sidewall_angle='0.0', sidewall_thickness='0.0', sidewall_k='0.0', surface_thickness='0.0', surface_k='0.0', bend_radius=None, num_modes='4', group_index_step='False', precision='double', grid_resolution='20', max_grid_scaling='1.2', cache_path='/home/runner/.gdsfactory/modes', overwrite='False', gap='0.2')
Effective indices: [2.51642926+4.72655552e-05j 2.49247523+4.48849401e-05j
1.90917889+2.00702360e-04j 1.80953208+2.20839326e-04j]
Mode areas: [0.26817256 0.26019659 0.65752823 0.60130012]
Coupling length: [32.35363595 7.77746926]