Path-length Analysis

This notebook demonstrates how to extract path-length and curvature from layout components.

Extract Path-length and Curvature from Components

In this section, we’ll extract the centerline from components and compute key metrics:

• Path-length between ports

• Minimum radius of curvature, \(R\)

• Maximum curvature (radius⁻¹), \(\kappa = \frac{1}{R}\)

For details on the curvature calculation, see Ref.\(~\)[1].

Show code cell source Hide code cell source

from IPython.display import display
import gdsfactory as gf
import matplotlib.pyplot as plt
import textwrap

from gplugins.path_length_analysis.path_length_analysis_from_gds import (
    extract_paths,
    get_min_radius_and_length_path_dict,
    plot_curvature,
)

Basic Example: Circular Bend

We start with a simple circular bend component to demonstrate the process.

c = gf.components.bend_circular()
path_dict, ev_path_dict = extract_paths(c, plot=True)
r_and_l_dict = get_min_radius_and_length_path_dict(path_dict)
for ports, (min_radius, length) in r_and_l_dict.items():
    print(
        textwrap.dedent(
            f"""
            Ports: {ports}
            Maximum curvature: {1 / min_radius:.2f}
            Minimum radius of curvature: {min_radius:.2f}
            Length: {length:.2f}
            """
        )
    )
    fig = plot_curvature(path_dict[ports])
    plt.show()
display(c.info)
difference_in_min_radius = abs(c.info["radius"] - min_radius) / c.info["radius"]
print(f"Relative difference in min radius: {difference_in_min_radius:.2%}")

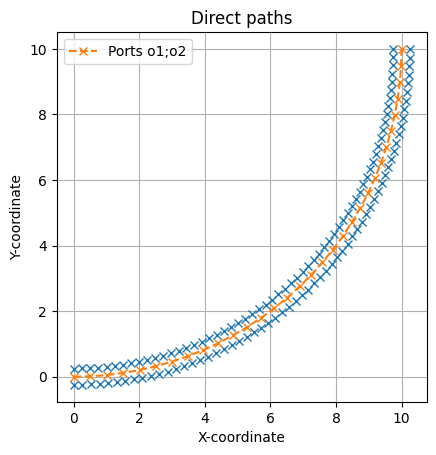
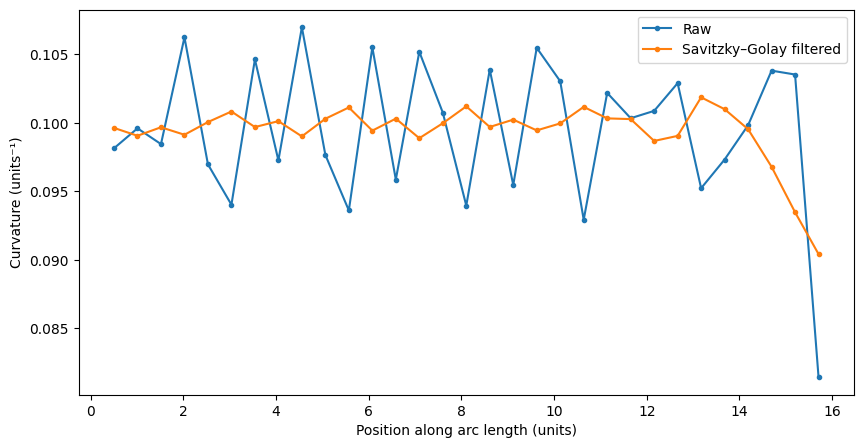
Ports: o1;o2
Maximum curvature: 0.11
Minimum radius of curvature: 9.35
Length: 15.71

Info(length=15.708, dy=10.0, radius=10.0, width=0.5, route_info_type='strip', route_info_length=15.708, route_info_weight=15.708, route_info_strip_length=15.708, route_info_n_bend_90=1.0, route_info_min_bend_radius=10.0)

Relative difference in min radius: 6.53%

Results for Different Number of Points

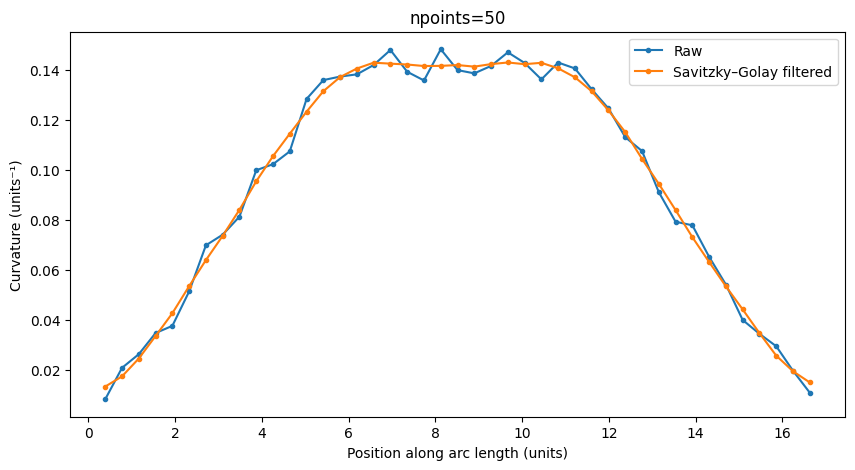
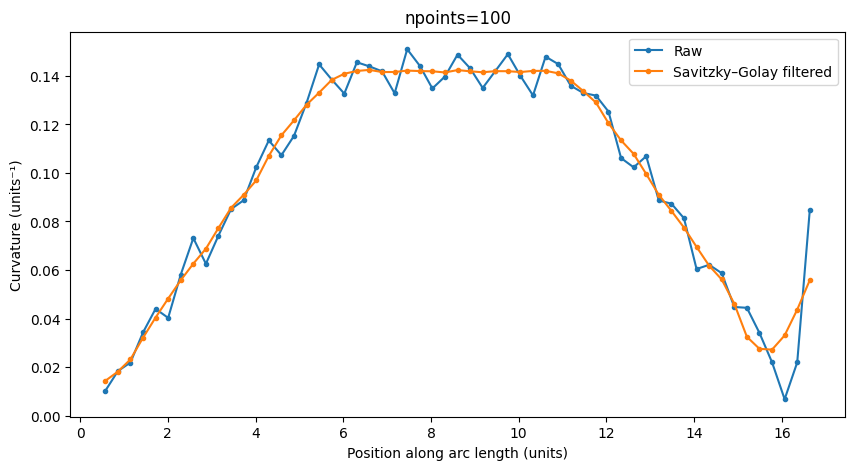
The accuracy of curvature calculations depends on the number of points used to define the component. Here, we show an Euler bend with varying number of polygon points (10, 50, 100 points) to observe how the calculated metrics change.

The smooth curvature transition of Euler bends should be better captured with higher point counts.

for npoints in [10, 50, 100]:
    c = gf.components.bend_euler(npoints=npoints)
    path_dict, ev_path_dict = extract_paths(c, plot=True)
    r_and_l_dict = get_min_radius_and_length_path_dict(path_dict)
    for ports, (min_radius, length) in r_and_l_dict.items():
        print(
            textwrap.dedent(
                f"""
                Ports: {ports}
                Maximum curvature: {1 / min_radius:.2f}
                Minimum radius of curvature: {min_radius:.2f}
                Length: {length:.2f}
                """
            )
        )
        fig = plot_curvature(path_dict[ports])
        plt.title(f"{npoints=}")
        plt.show()
    display(c.info)
    difference_in_min_radius = (
        abs(c.info["min_bend_radius"] - min_radius) / c.info["min_bend_radius"]
    )
    print(f"Relative difference in min radius: {difference_in_min_radius:.2%}")

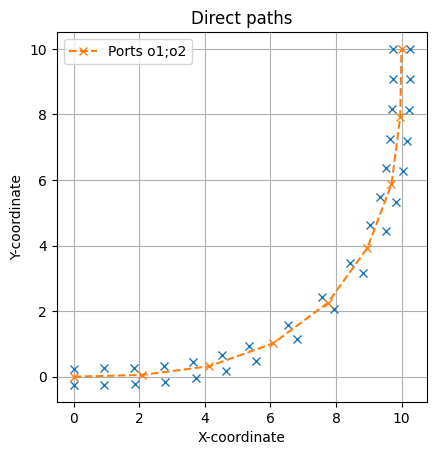
Ports: o1;o2
Maximum curvature: 0.15
Minimum radius of curvature: 6.88
Length: 16.59

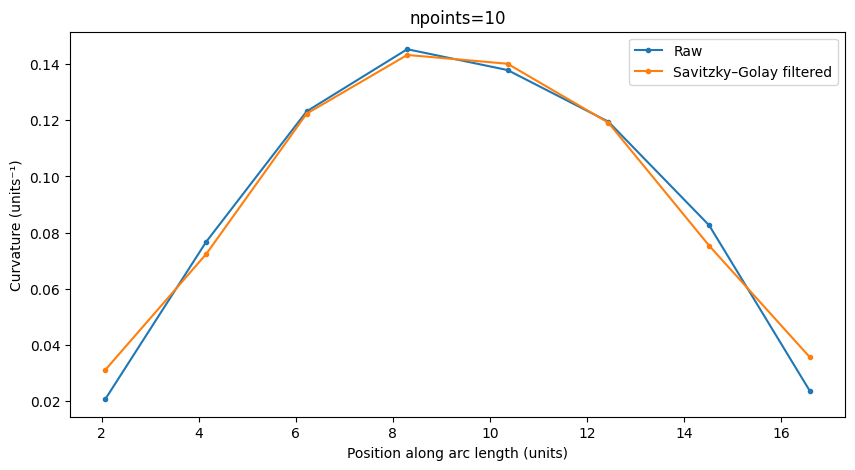
Info(length=16.625, dy=10.0, min_bend_radius=7.061, radius=10.0, width=0.5, route_info_type='strip', route_info_length=16.625, route_info_weight=16.625, route_info_strip_length=16.625, route_info_n_bend_90=1.0, route_info_min_bend_radius=7.061)

Relative difference in min radius: 2.55%

Ports: o1;o2
Maximum curvature: 0.15
Minimum radius of curvature: 6.75
Length: 16.64

Info(length=16.637, dy=10.0, min_bend_radius=7.061, radius=10.0, width=0.5, route_info_type='strip', route_info_length=16.637, route_info_weight=16.637, route_info_strip_length=16.637, route_info_n_bend_90=1.0, route_info_min_bend_radius=7.061)

Relative difference in min radius: 4.45%

Ports: o1;o2
Maximum curvature: 0.15
Minimum radius of curvature: 6.62
Length: 16.64

Info(length=16.637, dy=10.0, min_bend_radius=7.061, radius=10.0, width=0.5, route_info_type='strip', route_info_length=16.637, route_info_weight=16.637, route_info_strip_length=16.637, route_info_n_bend_90=1.0, route_info_min_bend_radius=7.061)

Relative difference in min radius: 6.20%

4-port component: directional Coupler

We can also handle components with:

• Multiple input/output ports

• An evanescent coupling region where light transfers between waveguides

The evanescent_coupling=True parameter enables analysis of the coupling regions.

c = gf.components.coupler()
path_dict, ev_path_dict = extract_paths(c, plot=True, evanescent_coupling=True)
r_and_l_dict = get_min_radius_and_length_path_dict(path_dict)
for ports, (min_radius, length) in r_and_l_dict.items():
    print(
        textwrap.dedent(
            f"""
            Ports: {ports}
            Maximum curvature: {1 / min_radius:.2f}
            Minimum radius of curvature: {min_radius:.2f}
            Length: {length:.2f}
            """
        )
    )
    fig = plot_curvature(path_dict[ports])
    plt.title(f"Ports: {ports}")
    plt.show()
display(c.info)
difference_in_min_radius = (
    abs(c.info["min_bend_radius"] - min_radius) / c.info["min_bend_radius"]
)
print(f"Relative difference in min radius: {difference_in_min_radius:.2%}")

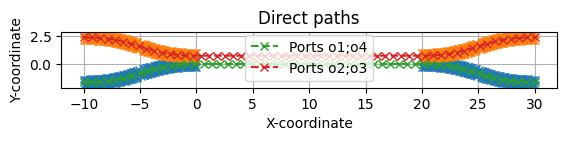
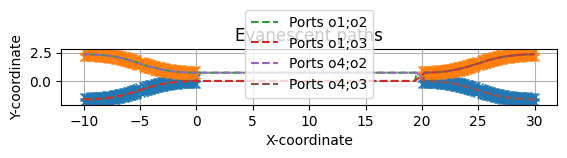
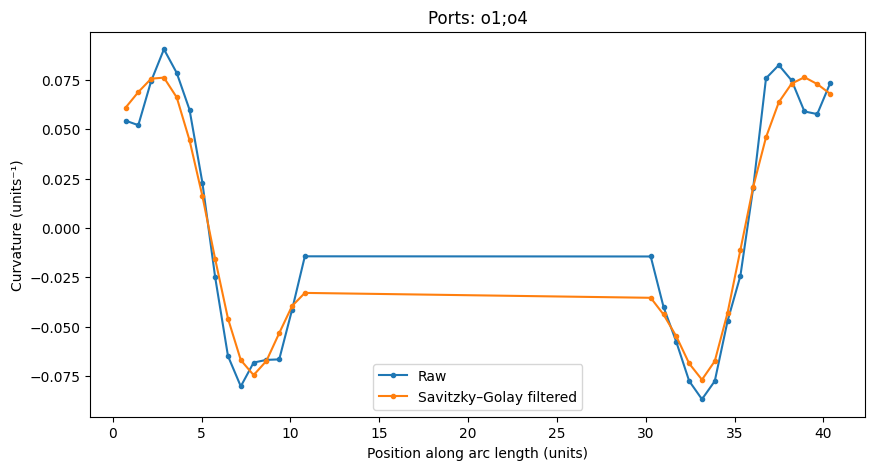
Ports: o1;o4
Maximum curvature: 0.09
Minimum radius of curvature: 11.04
Length: 40.37

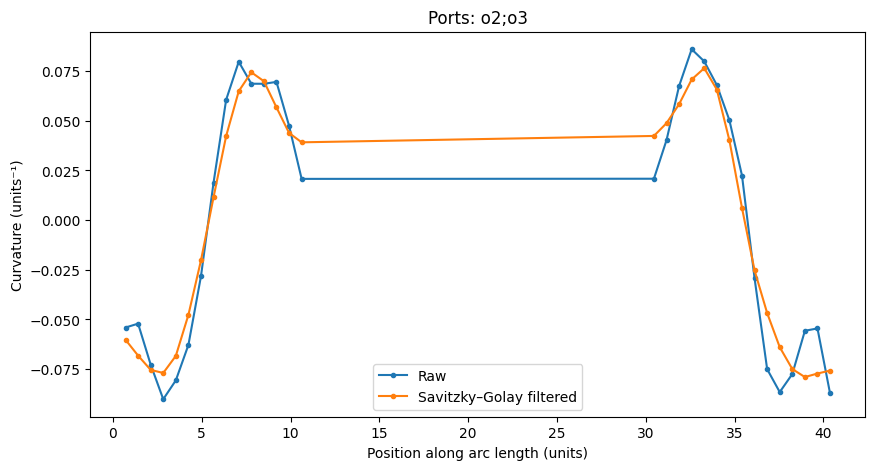
Ports: o2;o3
Maximum curvature: 0.09
Minimum radius of curvature: 11.09
Length: 40.37

Info(length=10.186, min_bend_radius=11.857)

Relative difference in min radius: 6.43%

Conclusion

This notebook demonstrates how to:

1. Extract path information from layout photonic components

2. Calculate important metrics (length, curvature)

3. Visualize the results

Bibliography

[1]

Eric W. Weisstein. Radius of Curvature. URL: https://mathworld.wolfram.com/RadiusofCurvature.html (visited on 2025-06-25).